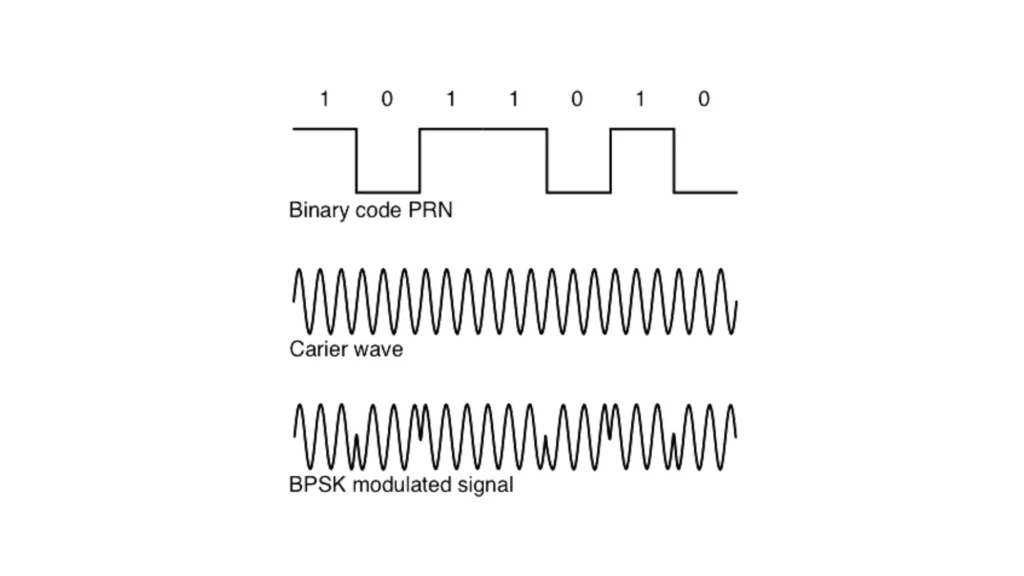
A Pseudo-Random Noise (PRN) code generates a binary sequence that appears random but remains deterministic and repeatable. Satellite navigation systems, such as GPS, Galileo, and BeiDou, along with various communication applications, rely on these codes.
PRN codes offer key characteristics that make them essential for navigation and communication.
They follow a deterministic pattern since algorithms generate them, ensuring precise reproduction. Despite their structured design, they exhibit statistical properties similar to white noise, making them appear random.
Engineers design different codes to be orthogonal or unique, which reduces cross-correlation and minimizes interference.
In GPS and GNSS applications (eg. Unmanned Aircraft Systems) , each satellite in the constellation transmits a unique PRN code.
These codes serve multiple functions: they help GPS receivers distinguish signals from different satellites, enable range calculation by comparing transmitted codes with a locally generated version to determine signal travel time, and support spread spectrum modulation.
This modulation technique allows signals to transmit over a wide bandwidth, increasing resistance to interference and jamming.
GPS uses different types of PRN codes. The C/A (Coarse/Acquisition) code supports standard GPS navigation and repeats every 1 millisecond. The P(Y) code, designed for military applications, encrypts its data and repeats every seven days.
The M-code, an advanced military version, enhances anti-jamming capabilities.
Linear Feedback Shift Registers (LFSRs) generate PRN codes, producing sequences with desirable correlation properties for precise signal tracking.
By maintaining pseudo-random characteristics while ensuring predictability and repeatability, LFSRs make these codes highly reliable for navigation and communication.
PRN Code Mathematical representation
For G1 and G2, the recurrence relation is:
G1(n) = G1(n−3) ⊕ G1(n−10)
G2(n) = G2(n−2) ⊕ G2(n−3) ⊕ G2(n−6) ⊕ G2(n−8) ⊕ G2(n−9) ⊕ G2(n−10)
Where ⊕ (XOR) is the binary addition operation.
The PRN code is then formed as:
PRN(n) = G1(n) ⊕ G2 (n+delay)
The delay varies for each GPS satellite, ensuring unique PRN sequences.